与面相切的线（接触面相切是不是就是平行）

1、与面相切的线

与面相切的线

每个人都有一个独特的外表。仔细观察，我们可以发现我们的脸上有许多与之相关的线条。这些线条看似微妙，但它们隐藏着丰富的信息，如我们的内在个性特征和生活财富。

印堂线

眉毛之间有一条穿过鼻梁的线，叫做印堂线。印堂线长而清晰的人大多头脑清晰，智商高，事业发展顺利。相反，印堂线短而模糊，容易遇到挫折和混乱。

法令纹

从鼻子两侧延伸到嘴角的两条线被称为法律线。法律线条深、长、清晰的人往往意志坚定、果断，容易成为职业生涯中的大工具。法律线条浅、模糊或中断的人犹豫不决，缺乏勇气。

眉尾线

眉尾有一条向下的线，叫做眉尾线。眉尾线低的人容易情绪低落，头脑细腻，注重情绪。相反，眉尾线高的人性格开朗外向，善于沟通。

人中线

鼻子下面有一条垂直线，叫做人中线。中线深、长、清的人身体健康、精力充沛、诚实。中线短浅、模糊的人容易虚弱、生病、敏感和多疑。

嘴角线

从嘴角两侧延伸到两侧的线称为嘴角线。嘴角向上的人乐观开朗，待人真诚友好。嘴角向下的人内向保守，消极悲观。

面部线条只是相学的一部分。只有通过综合分析其他因素，我们才能更准确地理解一个人的性格和财富。然而，通过观察这些与面部相关的线条，我们也可以获得一些有益的信息，提高我们对自己的理解，积极调整我们的心态，为生活的幸福奠定基础。

2、接触面是否平行？

接触面相切并不一定意味着平行。

接触面与平行的定义

接触面：当两个几何图形相交时，它们之间重叠的部分称为接触面。

平行：两个图形的线段或平面始终保持等距，不相互交叉。

接触面相切条件

两个图形的接触面相切有两个条件：

图形之间有公共点。

接触面的法线(垂直于切点的线段)相互平行。

满足这两个条件并不能保证图形是平行的，因为还需要满足以下条件：

若图形为平面，则接触面的法线必须垂直于接触面。

若图形为曲线，则接触面的法线必须沿曲线方向保持恒定。

不相交条件

如果两个图形不相交，即使它们的接触面相切，也不可能平行。这是因为平行图永远不会相交。

举例说明

例如，在以下两种情况下，接触面相切，但图形不平行：

相交线段：两条线段在某一点相交，但不平行。

相切圆:两个圆相切，但不平行。

因此，接触面切割不能保证图形平行，还需要满足额外的条件，如不相交与法线的关系。

3、线和面的切割是什么？

面与面相交有几条直线

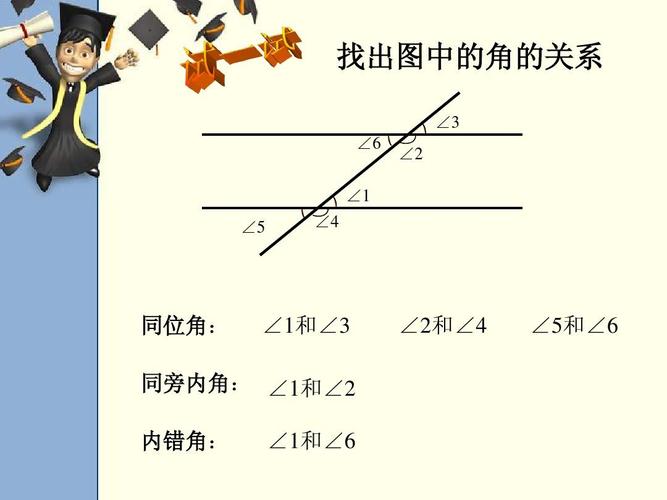
线与面相切是指一条直线与一个平面只在一个点上相交，形成一个点与平面之间的距离恒为零的情况。这种关系通常被称为相切关系。

相关关系在数学和几何学中具有重要意义。它通常用于描述各种形状和物体之间的关系。例如，在圆形中，切线是相对于圆周相切的直线。在多面体中，面与面之间的关系决定了多面体的整体形状和性质。

线与面相切的条件如下：

直线必须在平面的同一侧。

从直线到平面的任何距离都等于零。

直线与平面上的任何其他点都不相交。

当线与面相切时，可形成以下类型的相切关系：

内切线：在平面的同一侧切割直线和平面。

外切线：平面两侧直线与平面相切。

在现实生活中，线与面相切的情况也有很多应用，比如：

建筑：在建筑设计中，利用线与面的相关关系，可以创造出复杂美观的结构。

工程：在机械和土木工程中，用于分析和设计齿轮、轴承和支撑结构。

光学：在光学中，线与面之间的相切关系用于描述光的反射和折射行为。

线与面的切割是一种几何关系，描述了直线与平面只在一个点上交叉的情况。它具有重要的数学和实用意义，广泛应用于各个领域。

4、面与线相切是什么意思？

面与线的切割是指当一条直线与一个平面相交时，只有一个公共点。也就是说，直线与平面相交后，不会进入平面内部或从平面外部穿透。

要确定表面是否与线相切，可以观察直线与平面是否在相交点相切。如果直线与平面在相交点形成夹角，则表示直线与平面相切。

面与线相切的条件是：直线所在的直线族与包含平面的平面簇相切。直线族的参数方程为：

x = x0 λa

y = y0 λb

z = z0 λc

平面簇的参数方程为：

```

Ax By Cz D = 0

```

其中(x0， y0, z0) 是直线公垂线方程的点，(a, b, c) 是直线公垂线方程的方向量，(A, B, C) 为平面的法向量，D 是平面的常数。

相关条件如下：

```

Aa Bb Cc = 0

```

这种情况意味着直线族的公垂线与平面簇的法向量正交。