与正四面体的棱相切的球（若正四面体的棱长为a则其外接球的半径为）

1、与正四面体边缘相切的球

正四面体棱相切球，球心与正四面体各棱的距离相等。

从球心到正四面体各棱角的距离为r，正四面体棱角为a，球的半径为：

R = r a/2

r与a之间的关系可以通过几何计算找到:

```

r = (a√2) / (3 √2)

```

因此，正四面棱相切球的半径为：

```

R = (4a√2) / (3 √2)

```

球的体积如下：

```

V = (4/3)πR^3 = (64πa^3√2) / (27 9√2)

```

表面积为：

```

A = 4πR^2 = (128πa^2√2) / (27 9√2)

```

正四面体边缘切球与正四面体密切相关，其尺寸和体积与正四面体边缘成正比。

2、如果四面体的棱角为a，则外接球的半径为a

若正四面体的棱角为a，则外接球的半径为：

正四面体由四个相等的三角形组成，每个三角形的边长为a。根据正四面体的性质，四边的长度相等，每两边垂直相交。

外接球是与正四面体四个顶点相切的球体，其半径为从球心到正四面体顶点的距离。

设外接球的半径为r，从球心到正四面体顶点的距离也为r。正四面体对角线相等，长度为a√2.因此，从对角线中点到正四面体顶点的距离是a√2 / 2。

根据勾股定理，可得：

与正方体有关的球

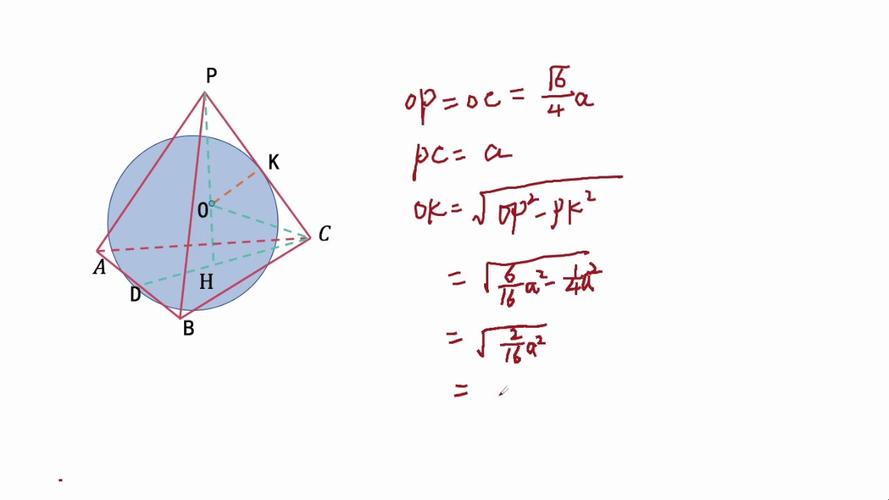
r2 = (a√2 / 2)2 (a / 2)2

r2 = a2 / 2 a2 / 4

r2 = 3a2 / 4

获得外接球的半径为：

r = √(3a2 / 4) = a√3 / 2

因此，如果正四面的棱角是a，则其外接球的半径是a√3 / 2。

3、如果四面体的棱角为a，则内切球的半径为a

若正四面体的棱长为 a，那么内切球的半径是：

证明：

设内切球的半径为 r，内切球与四面体各方交点与各顶点之间的距离为 r。四面体的顶点是 A、B、C、D，内切球与面 BCD 的交点为 E。

从正四面体的性质来看，∠ABC = ∠ACD = ∠ADB = ∠BDC = 109°28′16″。

则三角形 ABE 是等腰三角形，而且 BE = CE = r。

AB2由余弦定理 = AE2 BE2 - 2AE·BE·cos∠ABE。

由于 AB = a，AE = r，∠ABE = 109°28′16″，代入余弦定理：

a2 = r2 r2 - 2r2·cos109°28′16″

a2 = 2r2(1 - cos109°28′16″)

由此可得：

r2 = a2/4(1 - cos109°28′16″)

r2 = a2/4(1 1/4)

r2 = a2/2

r = a/√2

因此，如果正四面体的棱角是长的 a，内切球的半径为 a/√2。

4、与正四面体各面相切的球的半径

正四面体由四个全等的正三角形组成，每个面与其他三个面相交。如果一个球与正四面体的每个面相切，球的半径可以根据正四面体的边长计算。

将四面体的边长设置为 a，正四面体的棱长为 a√2.根据毕达哥拉斯定理，正四面体的高度为 a√2/2。

球与每个面的切点与正四面体顶点之间的距离是球的半径，设置为 r。根据勾股定理， ??：

(a√2/2)^2 = r^2 (r - a√2/4)^2

展开和简化，得到：

r^2 = a^2/8

因此，与正四面体各面相切的球的半径为：

r = a/2√2