球与圆锥的底面和侧面均相切（若圆锥与球的体积相等,且圆锥底面半径与球的直径相等）

1、球与圆锥的底面和侧面相切

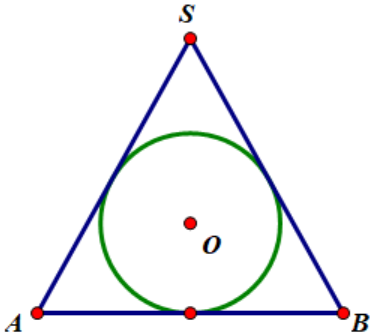
当球体与圆锥体的底面和侧面相切时，两者之间的几何关系非常有趣。

球体半径为r，锥体底部半径为R，底部中心与球心连接长度为d，高度为h。根据锥体侧面的性质，球体和锥体的侧面相切为一点（称为相切点）。该点与底部的距离为：

l = h - (R - r)

同时，根据相关关系，球心与圆锥底面的距离为：

```

d = R r

```

可以得到一个重要的关系类型：

```

h = l (R r)

```

根据勾股定理，可以得到一个关于底面半径、高度和底面与球心连接长度的等式：

```

(R r)^2 = d^2 (h - l)^2

```

代入上述公式，可得：

```

(R r)^2 = (R r)^2 (h - l)^2

```

简化后得到：

圆锥内切球半径与体积和表面积

```

h - l = 0

```

因此，当球体与圆锥体的底面和侧面相切时，球心与圆锥体底面的距离等于相切点与圆锥体底面的距离，即：

```

d = l

```

这意味着球心与圆锥底面在同一直线上，球体和圆锥体的侧面在相切点处形成切平面。

2、如果圆锥体的体积等于球，且圆锥体底部的半径等于球的直径

3、若圆锥的内切球(球面与圆锥的侧面和底面相切)

4、球和圆锥的底面和侧面是什么？

当球与圆锥的底面和侧面相切时，可以得出以下几点

1. 半径相等

球与锥体底部的切割意味着球的半径等于锥体底部的半径。同样，球与锥体侧面的切割意味着球的半径等于锥体底部到顶部的距离。

2. 切线垂直

球与圆锥相切点的切线垂直于圆锥的侧面和底部。这是因为切线总是垂直于切点的曲面法线。

3. 半圆柱相交

球与圆锥的切割形成半圆柱体，其半径等于球的半径，高度等于圆锥底面与顶点之间的距离。半圆柱体的中心轴与圆锥体的中心轴重叠。

4. 投影接触点

球与圆锥相切点的投影落在圆锥底面的中心和圆锥顶点的连接上。这是因为球的中心、相切点和圆锥的中心在同一平面上，垂直于圆锥的底面。

5. 几何构造

球与圆锥体的切割可用于几何结构，如确定圆锥体的体积或表面积。圆锥体的体积和表面积可以通过测量球的半径和半圆柱体的半径和高度来计算。