球与圆柱的底面和侧面均相切（球与圆柱的底面和侧面均相切图形）

1、球与圆柱的底面和侧面相切

球与圆柱体底部和侧面相切，形成几何学上称为“内切”的特殊关系。

球的半径是 r，圆柱底半径为 R，高为 h。球心与圆柱中心在同一条直线上，球心与圆柱中心的距离为 R。

通过勾股定理，可得：

(R - r)^2 h^2 = r^2

整理后得到：

```

h = ±√(2rR - r^2)

```

正号对应球心在圆柱底面以上的相切，负号对应球心在圆柱底面以下的相切。

当球与圆柱侧面相切时，球心与圆柱轴平行，球心与圆柱轴之间的距离为 R。球的半径 r 与圆柱底面半径 R 及高 h 它们之间的关系如下：

```

r^2 (R - r)^2 = h^2

```

整理后得到：

```

h = ±√(2Rr - R^2)

```

正号对应球心在圆柱侧以上的相切，负号对应球心在圆柱侧以下的相切。

当球与圆柱体底部和侧面相切时，球心位于圆柱体底部的中心轴上，球心与圆柱体轴之间的距离为 R。其高度 h 以上两个公式可以共同获得：

```

h = ±√(2rR - r^2) = ±√(2Rr - R^2)

```

由此可见，当球与圆柱体底部和侧面相切时，球的半径与圆柱体底部半径的关系与球心相对于圆柱体中心或圆柱体轴线的位置有关。

2、球的底部和侧面与圆柱形相切

球与圆柱相切

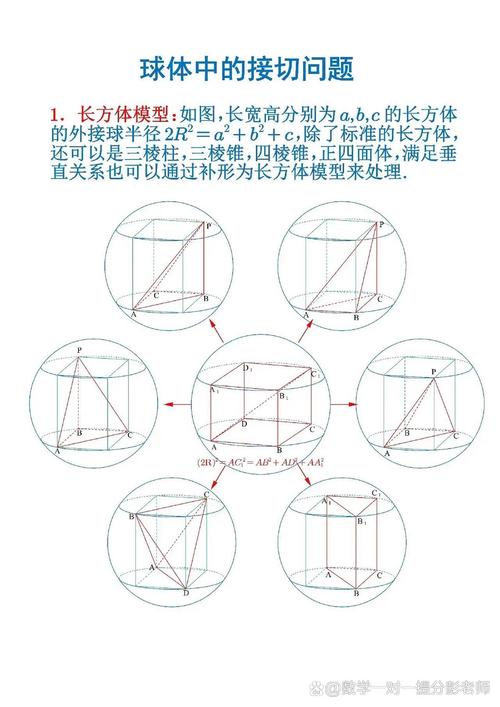
在一个空间几何图形中，当一个球与一个圆柱体相交时，会出现多种情况。特殊情况之一是球与圆柱体的底部和侧面相切。

当球与圆柱体底部相切时，球心位于圆柱体轴上，球半径等于圆柱体底部半径。此时，球的圆心与圆柱体的底部重叠。

当球与圆柱体侧面相切时，球心位于圆柱体表面，球的半径等于圆柱体母线段的长度。此时，球的中心位于圆柱体轴上，距离圆柱体底部的高度为球半径。

在这种情况下，球与圆柱体相切的部分是圆形的。这个圆的半径等于球的半径，圆心与球心和圆柱轴重叠。

球与圆柱体底部和侧面相切的图形具有以下特性：

圆柱体底面与圆柱体侧面的圆心重叠。

球半径等于圆柱底半径和母线段长度。

切圆半径等于球半径。

圆心位于球心与圆柱轴的交点处。

这种相切图形广泛应用于生活和工程中，如：

机械零件中的轴承和滑轮

建筑物中的穹顶和拱门

科学仪器中的透镜和反射镜

我们可以更好地理解和设计各种类型的空间，通过了解球与圆柱形底部和侧面相切的图形的性质 geomé从而在实践中发挥重要作用。

3、球与圆柱体的底面和侧面相切，对吗？

球和圆柱是否有底面和侧面同时切割是一个值得讨论的问题。简而言之，答案是否定的，没有这样的情况。

为了理解原因，让我们考虑一下球和圆柱体的几何形状。球是一个三维物体，由所有与固定点距离相等的点组成。圆柱体是一个三维物体，由两个平行圆盘组成，并连接到它们的侧面。

如果一个球与一个圆柱体的底面相切，这意味着球的表面在某个点与圆柱体的底面相遇。如果球的一侧也与圆柱体的一侧相切，这意味着球的曲面必须与圆柱体的曲面相交。这在几何学上是不可能的，因为圆柱体的曲面是由两条平行直线产生的，而球的曲面是弯曲的。

因此，球和圆柱体之间没有底部和侧面的切割。球的底部可以与圆柱体的底部相切，或者球的侧面可以与圆柱体的侧面相切，但不能同时发生。

4、球和圆柱的底面和侧面相切吗？

球与圆柱体的底面和侧面是否相切，取决于球与圆柱体的相对大小和位置关系。

当球的半径大于圆柱形半径时，球与圆柱形底面相切。此时，球的表面与圆柱形底面形成圆形接触面。然而，球与圆柱形侧面不相切。

当球的半径小于圆柱体半径时，球与圆柱体的底部和侧面不相切。球的表面在圆柱体内部，与圆柱体的底部和侧面保持一定的距离。

当球的半径等于圆柱形半径时，球与圆柱形底部和侧面相切。此时，球的表面与圆柱形底部和侧面接触形成圆形接触面。

具体来说：

当球的半径大于圆柱形半径时，球与圆柱形底面相切。球的表面与圆柱形底面形成圆形接触面，接触点位于圆柱形底面的中心。然而，球与圆柱形侧面不相切，球的表面在圆柱形内侧，与圆柱形侧面保持一定距离。

当球的半径小于圆柱体半径时，球与圆柱体的底部和侧面不相切。球的表面在圆柱体内部，与圆柱体的底部和侧面保持一定的距离。

当球的半径等于圆柱形半径时，球与圆柱形底部和侧面相切。球的表面与圆柱形底部和侧面接触形成圆形接触面，接触点位于圆柱形底部和圆柱形侧面。

因此，球与圆柱体的底面和侧面是否相切，取决于球与圆柱体的相对大小和位置关系。