平面相交的画法（平面与平面相交求交线的方法）

1、平面相交的画法

2、平面与平面相交求交线的方法

平面与平面相交的求交线

当平面与平面相交时，它们与一条直线相交，称为交线。求交线的方法有很多，主要有以下两种:

1. 三垂直线法

以这两条直线为边的平面，取两个平面中任意两条不平行的直线。

在这两个平面中，任意取两条垂直于交线的线段。

通过这两条线段的端点作为垂线，相交于交线上。

2. 断面法

任何一个与两个平面不平行的平面都称为横截面平面。

在截面平面上，两个平面分别截获两条直线。

这两条直线的交点是两条平面交线的投影。

两平面交线垂直于截面平面的投影，即两平面交线。

运用方法：

两平面方程或法向量根据问题的含义确定。

辅助平面或线段应根据求交线的方法建立。

求出交线的投影或端点，最后求出交线。

注意事项：

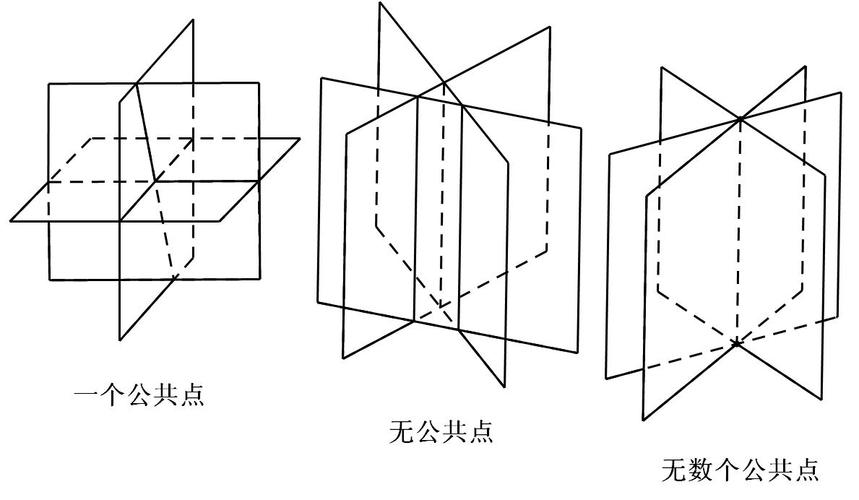
当两个平面平行或重合时，没有交线。

如果两个平面相互垂直，交线就是其中一个平面的垂线。

如果两个平面相交于一条已知的直线，那么交线就是这条直线。

3、平面相交的画法有哪些？

平面相交的画法主要有以下几种:

1. 直线与直线相交

平面相交的直线怎么求

两条直线重叠：画两条直线，使其重叠在同一位置。

两条直线相交：画两条直线，使其在某一点相遇，形成一个交点。

两条直线平行：画两条直线，使其永不相交，保持一定距离。

2. 直线与曲线相交

直线与圆相交：画一条直线，使其与圆的边缘相切或相交，形成一个或多个交点。

直线与椭圆相交：画一条直线，使其与椭圆边缘相切或相交，形成一个或多个交点。

直线与抛物线相交：画一条直线，使其与抛物线的边缘相切或相交，形成一个或多个交点。

3. 曲线与曲线相交

圆与圆相交：画两个圆，使其相交或相交，形成一个或多个交点。

圆与椭圆相交：画一个圆和一个椭圆，使其相切或相交，形成一个或多个交点。

圆与抛物线相交：画一条圆与一条抛物线，使其相切或相交，形成一个或多个交点。

在绘制平面相交时，应注意以下几点：

确保交点准确，交线角度和比例正确。

区分相切和相交的情况，相切时两条线没有交点，相交时有交点。

灵活运用圆规、直尺等工具，准确地绘制出各种形状的平面交叉。

4、平面与平面相交的绘画方法

平面与平面相交的画法

在空间几何中，平面与平面的交叉通常形成一条直线。为了准确地画出平面与平面交叉的直线，需要遵循以下步骤：

1. 确定两个相交平面:确定空间中两个相交平面。一个平面可以用两条相交的直线或两条平行于同一条直线的平面来定义。

2. 找到相交直线：观察两个平面，找出它们相交的直线。这条直线可以是有限的或无限的，垂直于两个平面的法线。

3. 垂直线：从一个平面上的任何一点到另一个平面。垂直线的端点将落在交叉直线上。

4. 连接点:将垂直线的端点与另一个平面上的任何一点连接起来，形成一条直线。这条直线平行于交叉直线和两个平面。

5. 确定相交点：相交直线与连接线之间的交点是平面与平面之间的交点。

注意：

若两个平面平行，则无相交点。

若两个平面垂直，则交叉直线为无限直线。

根据两个平面的位置，相交直线可以是线段、射线或直线。