两相交的立体的表面交线称为什么（两立体相交相贯线为封闭的空间曲线特殊情况为平面曲线）

1、为什么两相交的三维表面交线被称为

当两个立体相交时，它们表面的交线称为棱线。

棱线是连接两个三维表面交叉点的直线段。棱线是一个非常重要的概念，因为它可以帮助我们确定三维形状的大小和形状。

我们可以通过观察边缘和线来了解两个三维的相对位置。例如，如果两个正方体的边缘是平行的，那么它们是平行的；如果两个正方体的边缘交叉成直角，那么它们是垂直的。

棱线的形状也取决于相交的两个三维。例如，如果两个立方体相交，它们的棱线将是直线段；如果一个球体与一个圆柱体相交，它们的棱线将是圆弧。

棱镜对于确定三维表面积和体积也非常有用。例如，棱镜的表面积等于其底面积和所有侧面积，侧面积等于其高度乘以棱镜的周长。

边缘线是由两个三维交叉形成的表面交叉线。它是一个重要的几何概念，可以用来确定三维形状的大小、形状、相对位置、表面积和体积。

2、两立体相交相贯线为封闭空间曲线的特殊情况是平面曲线

3、两立体相交，三维表面得到的交线是( )

凹曲线和凸曲线平面图

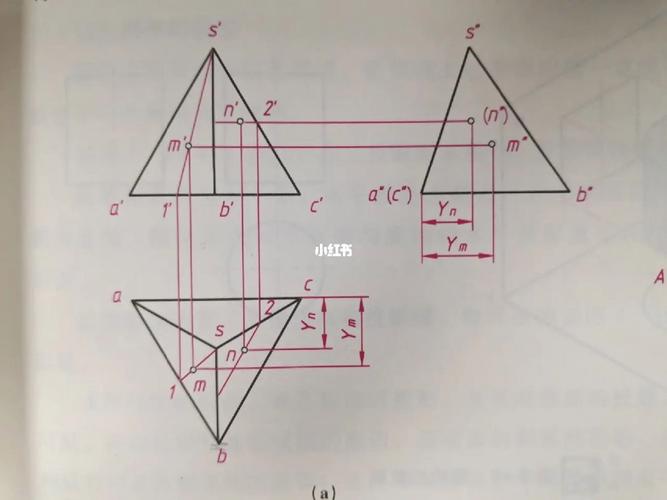
当两个立体相交时，从立体表面获得的交线称为交线。交线是连接两个立体相交点的空间曲线。

交叉线的性质取决于交叉两个三维表面的类型。当两个平面相交时，它们的交叉线是一条直线。当一个平面与一个曲面相交时，它们的交叉线是一条曲线。当两个曲面相交时，它们的交叉线可能是一条曲线或一个点集。

交叉线可以用来描述两个三维之间的关系。例如，交叉线可以用来确定两个三维是否相切或相交。交叉线也可以用来计算两个三维之间的交叉面积或体积。

在工程和设计中，交叉是一个重要的概念。在建筑设计中，交叉可以用来确定不同建筑部件之间的关系。在产品设计中，交叉可以用来优化产品的形状和功能。在制造业中，交叉可以用来确定不同部件之间的合作关系。

当两个三维交叉时，从三维表面获得的交叉线是连接两个三维交叉点的空间曲线。交叉线的性质取决于交叉两个三维表面的类型。交叉线在工程和设计领域有着重要的应用。

4、当两个几何表面相交时，在两个三维表面

当两个几何表面相交时，它们形成一条叫做相交线的空间曲线。在两个三维表面上，相交线将两个表面划分为不同的区域。

在相交点的邻近区域中，两个表面共有的区域称为重叠区域。重叠区域的形状和大小取决于相交曲线的形状和相交点两个表面的曲率。

交叉线外的区域是两个表面各有的区域。对于给定的表面，交叉线将表面分为两个不相交的区域，称为外部区域和内部区域。

外部区域是指位于相交线外的区域。外部区域由两个表面之间的间隙组成，形状由两个表面之间的相对位置决定。

内部区域是指位于相交线内的区域。内部区域被一个表面包围，另一个表面从内部分离。内部区域的形状由周围区域的表面决定。

交叉线、重叠区域、外部区域和内部区域是两个几何表面交叉的重要几何特征。这些特征广泛应用于工程、设计和拓扑领域。例如，它们可以用来计算两个物体之间的接触面积，分析结构的强度，或研究几何拓扑的性质。