两平面相交,交线是什么（两平面相交交线是什么一平面与一个曲面相交,交线昰）

1、两个平面相交，交线是什么？

两个平面交叉，它们的交叉线是一条直线。这是因为两个平面由两条非平行直线确定，而两条非平行直线只交叉一点。因此，两个平面的交叉线是两条直线的交叉点。

交叉线的性质取决于两个平面之间的位置关系。如果两个平面相交于直角，则交叉线垂直于两个平面。如果两个平面相交于任何角度，则交叉线斜交于两个平面。

交叉线也可以用两个平面的法线来表示。法线是垂直于平面的直线，并通过平面上的任何点。两个平面的交叉线与两个平面的法线平行。

了解两个平面交叉的交叉线对于解决空间几何问题非常重要。例如，我们可以使用交叉线来解决两个平面的两个角，或者解决空间中两条直线之间的夹角。

2、什么是两个平面的交线？一个平面与一个曲面相交，交线

3、两个平面的交叉线是什么？平面和一个曲面的交叉线是什么？

4、两平面相交的交线是两平面

两个平面相交的交线平行于平面吗

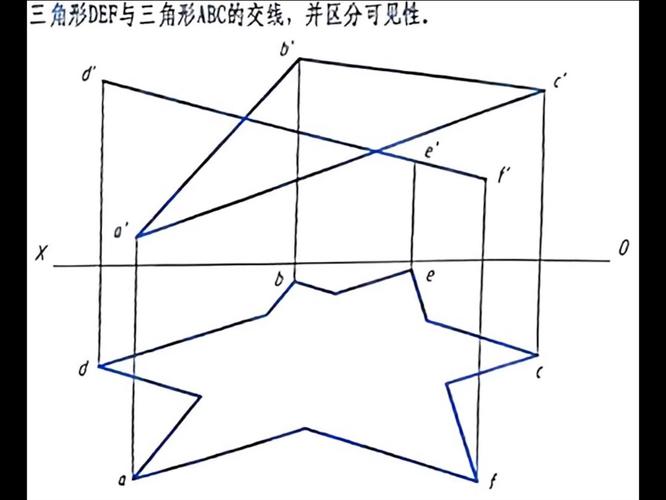
两个平面相交，交线为直线。这一定理阐述了平面几何中两个平面交叉的基本性质，即两个平面交叉，它们的交叉必须是一条直线。

证明：

设平面α和β相交，它们的交线是l。取α上面任何一点A，β任何一点B，连接AB。因为AB的两端都在α和β所以AB在α和β上，即AB是α和β公共部分。

假设α和β不止一条交线，即另一条直线m满足m也存在α和β然后，m和l有一个公共点，这与直线不能相交于两点以上。因此，α和β只有一条交线。

推论：

以下推论可以从这一定理中推出：

两平面相交的交线通过两平面上的任意两点。

两平面相交的交线平行于两平面中的任何一条公垂线。

假如两个平面相交，那么两个平面的任何一条垂线都在交线上。

应用：

在几何学和工程学中，两平面相交的交线被广泛应用于几何学和工程学中，如：

解决直线与平面的交点。

确定两个平面之间的夹角。

在建筑结构中设计平面连接。