相交的平面把空间分成几个部分（相交的平面把空间分成几个部分怎么画）

1、相交的平面将空间分成几部分

相交平面将空间划分为不同的部分，具体部分的数量取决于相交平面的数量及其相交方式。

最简单的情况是两个交叉平面，它们将空间分为四个部分：正八面体、两个四面体和一个中心棱柱。

当更多的平面相交时，划分区域的数量会迅速增加。例如，三个交叉平面将空间分为八个区域，四个交叉平面分为16个区域，等等。

值得注意的是，一些交叉平面可能不会将空间完全划分为不同的区域。例如，如果两个平面平行，它们只会将空间划分为两个半空间。

相交平面广泛应用于几何和应用数学中。例如，它们用于确定多面体的体积或计算两个曲面之间的距离。在建筑和工程领域，相交平面用于设计和分析复杂的结构。

交叉平面可以通过多种方式将空间划分为不同的部分，具体数量取决于交叉平面的数量和交叉方式。这些区域在几何学和应用数学中得到了广泛的应用。

2、交叉平面如何将空间分成几个部分？

将空间划分为相交平面

当两个平面相交时，它们将空间分为几个部分。理解这些部分对于理解几何图形非常重要。

两个平面相交时，形成四条直线：

两条相交线，即两个平面相交的线段

两条与相交线平行的线称为平行线

这四条线将空间分为八个部分：

1. 两个半空间

位于相交线一侧的两个区域称为半空间。

2. 四个二面角

交叉线周围形成的四个角形区域称为二面角。

3. 相交平面本身

两个平面相交的部分称为相交平面。

4. 边线

相交平面与半空间与二面角的交线称为边线。

要绘制这些部分，请遵循以下步骤：

1. 绘制两个相交平面。

2. 确定交叉线。

3. 画出与相交线平行的平行线。

4. 将空间分为八个部分。

对于解决几何问题和可视化空间关系，理解相交平面划分空间的部分非常重要。

平面与平面立体相交怎么画图

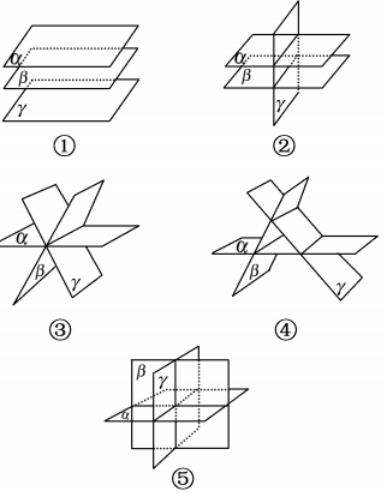
3、两个相交的平面将空间分成几个部分

两个相交平面将三维空间划分为不重叠的区域。以下是由此划分的空间部分：

正半空间 A：它包含与第一个平面同侧的点。

正半空间 B：它包含与第二个平面同侧的点。

负半空间 C：包括位于两个平面另一侧的点。

交线 L：两个平面的交集是一条直线。

交角 D：尖角由两个平面形成，顶点位于交线上。

具体而言：

任何一点位于正半空间 A 或正半空间 B，但不能同时位于两个正半空间。

位于交线 L 上点不仅属于第一个正半空间，也属于第二个正半空间。

位于交角 D 内部点属于第一个正半空间和第二个正半空间。

负半空间 C 由两个平面以外的点组成。

在各种应用中，两个相交平面形成的分隔区具有重要意义，例如：

几何：确定空间中点、线和面的相对位置。

微积分：计算体积和积分。

物理学：建模电磁场和流体力学。

工程：设计结构和机械元件。

了解相交平面划分的空间区域有助于解决空间关系和几何特征的问题。

4、相交的平面将空间分成几部分图片

交叉平面将空间分成几个部分的原理并不复杂，但它需要一些空间想象力来理解。当两个平面相交时，它们形成一个叫做“交叉线”的公共线段，而交叉线所在的平面称为“交叉平面”。

交线将两个平面分为四个不同的部分：

交叉部分：这是位于交叉线两侧的两个平面重叠部分。

不相交部分：这是位于交线两侧的两个平面无重叠部分。

上半部分:这是两个平面上方的空间部分，不包括交线。

下半部分:这是两个平面下方的空间部分，不包括交线。

因此，两个相交平面将空间分为六个不同的部分：两个相交部分，两个不相交部分，两个半部分。

为了更好地理解这个概念，你可以想象两个平面代表一张桌子和一张放在桌子上的纸。桌子与纸相交的公共线段是桌子的边缘，交叉线所在的平面是桌子的表面。

相交部分是桌子表面覆盖纸的部分，不相交部分是桌子表面没有被纸覆盖的部分。上半部分是桌子和纸的顶部，不包括桌子或纸边的空间部分，下半部分是桌子和纸的底部，不包括桌子或纸边的空间部分。

通过这个比喻，我们可以更直观地理解交叉平面如何将空间分成不同的部分。