棱锥的侧面都相等吗（棱锥的侧面不一定是三角形这句话对吗）

1、棱锥的侧面等吗？

棱锥的侧面是否相等取决于棱锥的类型。

正棱锥

在正棱锥中，侧面是等腰三角形。正棱锥的底面是规则的多边形，侧面垂直于底面。因此，正棱锥的所有侧面都是相等的。

非正棱锥

在非正棱锥中，侧面不一定相等。侧面可以是不同的三角形、梯形或其他形状。例如：

斜棱锥:侧面不等腰三角形，不垂直于底面。

扭棱锥：其侧面为扭曲的三角形，形状不规则。

例外情况

有一种特殊的非正棱锥，其侧面可相等：

等腰棱锥：其侧面为全等二等腰三角形。等腰棱锥的底面为矩形，侧面与底面交叉在底面的中点。

因此，一般来说，棱锥的侧面不一定相等。只有正棱锥和等腰棱锥的侧面相等。

2、棱锥的侧面不一定是三角形，对吗？

棱锥的侧面是否一定是三角形，需要根据棱锥的具体形状来判断。

一般来说，棱锥的侧面确实是三角形的。这是因为棱锥是由一个底部和多个三角形侧组成的。底部可以是任何多边形，侧面由底部的边缘和连接到底部的顶部组成，因此为三角形。

然而，也有一些特殊情况，棱锥的侧面不是三角形。例如：

四棱锥：四棱锥底面为正方形，侧面为四个等腰梯形。

五棱锥：五棱锥的底面为正五边形，侧面由底面的边缘和与底面相连的顶点组成，因此为平行四边形。

六棱锥：六棱锥的底面为正六边形，侧面由底面的边缘和与底面相连的顶点组成，因此为梯形。

将一个棱锥分成四个小棱锥

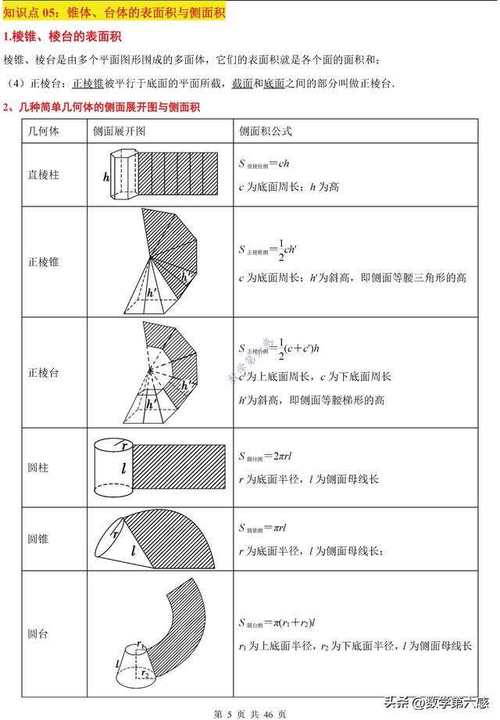
因此，棱锥的侧面是否必须是三角形需要具体分析。一般来说，它是三角形，但在特殊情况下，它不是三角形。

3、棱锥的边缘长度相等，对吗？

棱锥的边缘长度是否相等取决于棱锥的底面形状。

如果棱锥的底部是正多边形，那么棱锥的所有边长都是相等的。这是因为正多边形的边长是相等的，棱锥的边缘与底部和顶点相连，所以棱锥的边长也是相等的。常见的等边棱锥，如正三棱锥、正四棱锥等，都属于这种情况。

如果棱锥的底面为非正多边形，则棱锥的侧边长度可能不相等。例如，如果棱锥的底面为三角形，则底面的长度不同，导致连接底面和顶点的侧边长度不同。

为了进一步理解这一点，我们可以考虑一个底部为正三角形的棱镜。由于底部边缘的长度不同，这个棱镜的三个边缘长度可能不同。如果棱镜垂直切割成两部分，其中一部分将是一个正三角形的棱镜，其边缘长度相等。

因此，棱锥的侧边长度是否相等取决于棱锥底面的形状。对于底面为正多边形的棱锥，其侧边长度相等；对于底面为非正多边形的棱锥，其侧边长度可能不相等。

4、棱锥的侧面是曲面还是平面

菱锥侧面是否为曲面或平面，取决于菱锥的类型。

规则菱锥

规则菱锥的底面为多边形，由三角形组成。这些三角形位于底面周围，连接底面中心和每个顶点。规则菱锥的侧面为平面。

不规则菱锥

不规则菱锥的底面不是多边形的，其侧面可以由任何三角形或四边形组成。不规则菱锥的侧面可以是平面或曲面。

曲面侧面

如果菱锥的底面不平整，或者侧面不完全平整，则菱锥的侧面为曲面。例如，如果菱锥的底面是圆形的，则侧面是锥形的表面。

平面侧面

如果菱锥的底面是平的，侧面是完全平的，那么菱锥的侧面就是平的。规则菱锥就是平面侧面的例子。

因此，菱锥的侧面是曲面还是平面取决于菱锥的类型。规则菱锥的侧面是平面，而一些不规则菱锥的侧面可能是曲面。