投影面平行线同时与几面投影相交（投影面平行线与投影面的位置关系是什么）

1、投影面平行线与几面投影相交

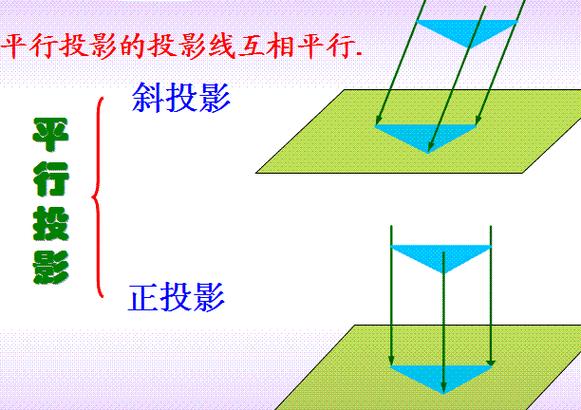
投影平行线与多面投影相交

在工程绘图中，正交投影是表示物体几何形状的常用方法。在三视图投影中，物体上的平行线投影到三个投影面（前、侧、平面）上，形成平行线。

当投影面与物体上的某个平面平行时，平面的平行线将同时与所有投影面相交。例如，如果物体有一个平行于正投影面的平面，则平面上的所有平行线将同时投影到正面、侧面和平面投影上，并在每个投影面上形成一对平行线。

根据投影原理，平行于投影表面的平行线在投影表面上投影为等长的平行线。因此，当投影平行线同时与几个投影相交时，这些平行线在每个投影表面上的投影长度相等。

这种性质在工程图纸中非常重要。它可以用来确定物体的大小、形状和位置关系。例如，通过测量投影表面平行线的长度，可以确定投影表面平行线的大小。通过分析平行线在各投影表面的相对位置，可以确定物体的倾斜角度和空间位置。

同时，投影面平行线与几面投影相交的性质广泛应用于工程制图中，可以帮助设计师准确表达物体的几何形状和空间关系。

2、投影面平行线与投影面位置的关系是什么？

投影平行线与投影平行线的位置关系：

当一条直线平行于一个平面时，它们的投影线平行。

定理：

若一条直线与平面平行，则其任何投影线均与平面平行。

证明：

假设直线 l 与平面 α 平行，过 l 上一点 P 作 l 的投影线 PQ，且 PQ 交 α 于点 Q。

由于 l 与 α 平行，因此 l 以上任何一点(比如 P）到 α 距离相等。

因此，△PQA 和 △PQC 中，PA = PC（到 α 距离相等)，QA = QC（投影线 PQ）

并且，∠PAQ = ∠PCQ（因为 l 与 α 平行）

平行线培优题100题

所以，△PQA ≌ △PQC（SAS 全等）

这意味着 PQ 与平面 α 平行（因为 PQ 公共垂直线是两条平行线)。

因此，l 任何投影线都平行于平面 α。

3、有几条投影反映了投影平行线的实际长度

投影面的平行线投影反映了长条数

当平行于投影面的线在空间中投影到投影面时，其投影长度通常不等于原始长度。只有当平行线满足特定条件时，其投影才等于长度。

投影反映了长度的条件：

投影射线平行：平行射线与投影射线的夹角为 90 在这种情况下，投影长度等于实长。

与投影面平行：平行线位于投影面内，与投影面重合，投影长度等于实长。

在其他情况下，投影长度与实长的关系：

平行线倾斜于投影射线：投影长度将比实际长度更长，缩短程度由倾斜角决定。

除上述特殊条件外，平行线与投影面相交：除非满足上述特殊条件，否则投影长度通常不等于实长。

应用：

在建筑和工程设计中，了解平行线投影的性质是非常重要的。例如，在投影图中，平行于投影方向的线可以准确地表示其长度，而倾向于投影方向的线需要考虑投影带来的长度缩小。

在测量中，当测量对象和测量工具倾斜时，还需要考虑投影长度和实长之间的差异，以确保测量的准确性。

4、投影面平行线只平行于投影面