平面与曲面相交得到什么（平面和曲面相交时,组合体相交处有截交线,并且为直线）

1、什么样的平面与曲面相交？

当平面与曲面相交时，形成的交线类型取决于曲面的形状和与平面相交的位置。具体来说:

平面与球面相交：

若平面与球心的距离小于或等于球面半径，则交线为圆。

若平面与球心的距离大于球面半径，则交线为空集。

平面与圆柱面相交：

若平面与圆柱轴平行，则交线为直线。

如果平面垂直于圆柱轴，并通过圆柱中心，则交叉线为直径。

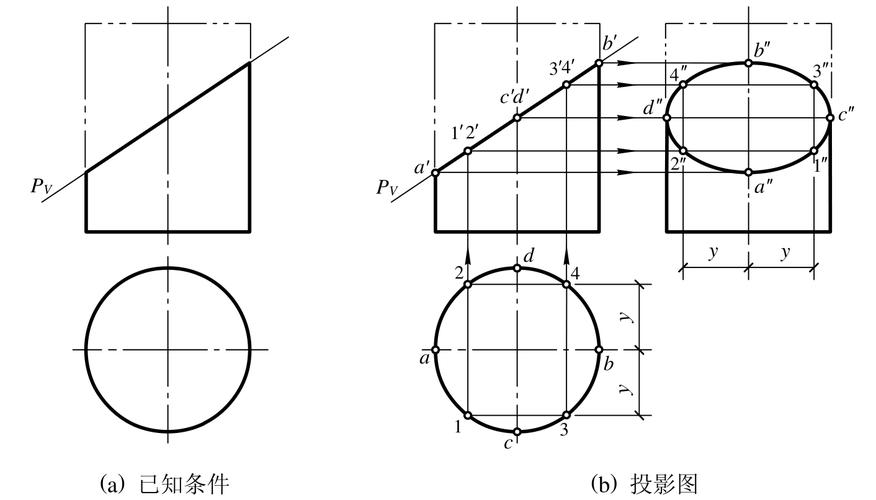
若平面与圆柱轴既不平行也不垂直，则交线为椭圆。

与圆锥面相交的平面：

若平面与圆锥轴平行，则交线为圆。

若平面垂直于圆锥轴，并通过圆锥顶点，则交线为三角形。

若平面与圆锥轴不平行或垂直，则交线为圆锥曲线，如椭圆、抛物线或双曲线。

平面与其它曲面相交：

对于其他更复杂的曲面，平面与曲面交叉的交叉线形状将更加复杂。例如，当平面与椭球面交叉时，交叉线可能是椭圆、圆或其他曲线。当平面与双曲面交叉时，交叉线可能是双曲线或抛物线。

机械截交线的含义

平面与曲面的交叉取决于曲面的形状和平面与曲面的交叉位置。这些交叉形状广泛应用于数学和工程学中，如解决几何问题、绘制图形和设计结构。

2、平面与曲面相交时，组相交处有截交线，为直线

当一个平面与一个曲面相交时，它们相交的几何形状称为截交线。有趣的是，无论曲面有多复杂，截交线总是一条直线。

这是因为平面可以看作是由无数相互平行的直线组成的。当平面与曲面相交时，曲面上的每个点都会与平面上的直线相交。连接这些交点的线段是截交线。

这种性质在几何学中有许多重要的应用。例如，它可以用来解决三角形和四边形的面积和体积。它还可以用来解决圆柱体、圆锥体和球体的几何问题。

为了证明截交线永远是一条直线，我们可以使用解析几何。假设平面由方程组成 $ax by cz=d$ 给出，曲面由方程制成 $f(x,y,z)=0$ 给出。然后，截交线上的点必须同时满足这两个方程。

例如，我们可以消除平面方程中的一个变量 $z$。这将获得一个新的方程，截交线上的点必须同时满足新的方程和曲面方程。

新方程的阶数是 $2美元，这意味着它代表一个平面。因此，截交线必须位于这个平面上。由于截交线是平面的子集，因此必须是直线。

因此，我们已经证明，当一个平面与一个曲面相交时，它们的相交处总会有一条截交线，截交线总是一条直线。

3、曲面与平面相交可能是一条直线

4、平面与曲面相交的线是什么？